Recently I've got asked, how would I pseudocode the following number division exercise:

- Search a string of at least five numbers (for example, 37540).

- Identify all of the substrings that form numbers that are divisible by 3.

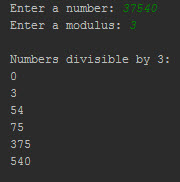
- For example, applying the algorithm on the string 37540 should produce the following substrings: 0; 3; 54; 75; 375; 540

Intro

To make this task a bit more challenging, I’ve designed a pseudocode that takes two initial parameters:

- **Any Number** (e.g. 37540)

- **Any Divider** (e.g. 3)

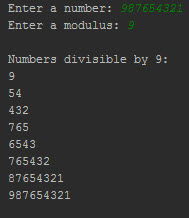
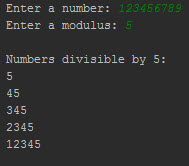
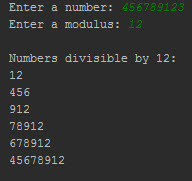
Once above parameters are set, script automatically identifies all substrings that form numbers that are divisible by the set divider. During the calculation, all numbers are stored in an array, that is at the end sorted in an ascending order (for the number: 37540 and a divider: 3, it outputs: 0; 3; 54; 75; 375; 540)

To accomplish the task, I’ve used a mathematical formula for modulus operation. In computing, the modulus operation (or modulo) finds the remainder after the division of two numbers. Modulus is typically calculated using following formula (a is initial number, n is a divider):

a - (n * int(a/n))

This basically means, that the number is divisible by the set divider, as long as the result of above formula = **0 **(meaning, there is no reminder).

Let me illustrate modulus operation, by trying to find out if number 54 is divisible by 3. Follow me, this is really simple!

All we need is to calculate the modulus 3 of number 54. As long as the result is 0, the number is divisible by 3.  So let’s find out!

a - (n * int(a/n))

54 - (3 * int(54/3))

54 - (3 * 18)

54 – 54 = 0

Yes, the final result = **0 **(meaning, the number 54 is divisible by 3)

Pseudo-Code

So, here is the pseudo-code that uses modulus operation to find all divisible number for any given number and divider.

To make the pseudocode better:

- All variables are initialized upfront

- All lines of the pseudocode are numbered

- All FOR loops are named

- All IF conditions are named

- All references for FOR AND IF steps now refer to their starting line numbers

- Steps are color coded for easier reading

JAVA Proof

It was very simple to create a JAVA algorithm that accepts a modulus parameter and that way the code now calculates any division for any number. Here is the working code:

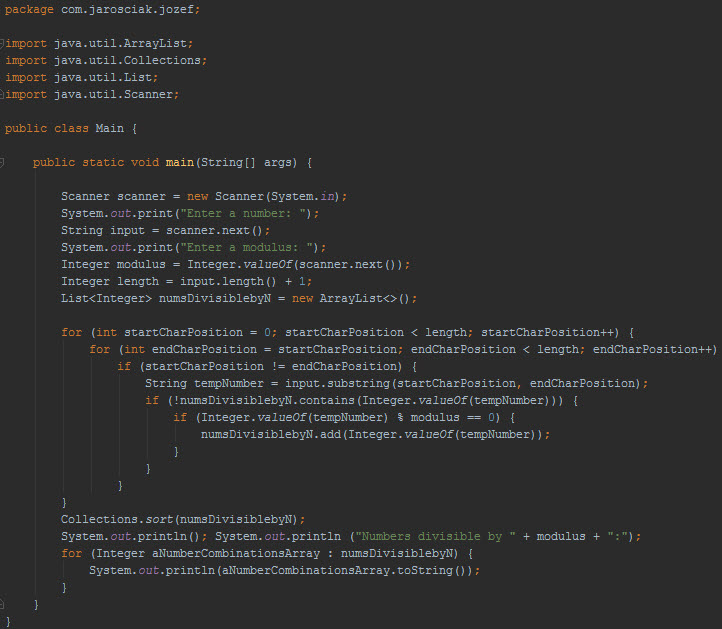
And couple of examples of the outputs: