JavaScript n-Block Tangram Puzzle Solver

📅 Published 03.01.2018
🏷️ Software Development
Recently I found a tangram puzzle made of polyomino (triominoes, tetrominoes and pentominoes) which caught my attention. The goal of the puzzle was to rotate the blocks in such a...

Recently I found a tangram puzzle made of polyomino (triominoes, tetrominoes and pentominoes) which caught my attention. The goal of the puzzle was to rotate the blocks in such a way, so they fit into the 10 x 6 rectangle box.

This is the puzzle:

It occurred to me, that it's a good problem to solve the puzzle programmatically. The following is my attempt at doing s0 using JavaScript:

I have created the Block Puzzle Solver that calculates the solutions to monomino, domino, triomino, tetromino and pentomino(1) based rectangular or square tangram puzzle in a user-defined area, with support for block rotation and reflection. The fast version uses a random unique block combination. The slow version tests all possible block combinations and permutations (there can be quite a lot of them). The plan for the future is to include more pentominoes, heptominoes, octominoes & other polyominoes; as well as support user-defined areas of any shape.

 

Source Code: Github

Online Demo at https://www.joe0.com/blockpuzzlesolver.com/

 

Screenshot:

This is the screenshot of the solution for exactly the same puzzle configuration in the picture above:

And here is a screenshot for using **38 **Blocks (A,A,A,A,A,A,A,A,A,A,B,B,B,B,B,B,B,B,C,C,C,C,C,C,D,D,I,I,L,L,O,O,S,S,T,T,X,X) on a 10 x 10 board. The puzzle was solved in 27.6s seconds on Pentium I7, even though there is 17,179,869,184 block combinations in the given order only. It's altogether 666,368,255,568,059,000,000,000,000,000,000,000,000 distinct block permutations (math explained here). The chance of finding the solution is always dramatically improved by using monominoes or dominoes. The random approach appears to be the winner in most cases. However, it doesn't guarantee the solution, whereas going through all combinations do (if there is one), but it takes exponentially longer to solve the puzzle.

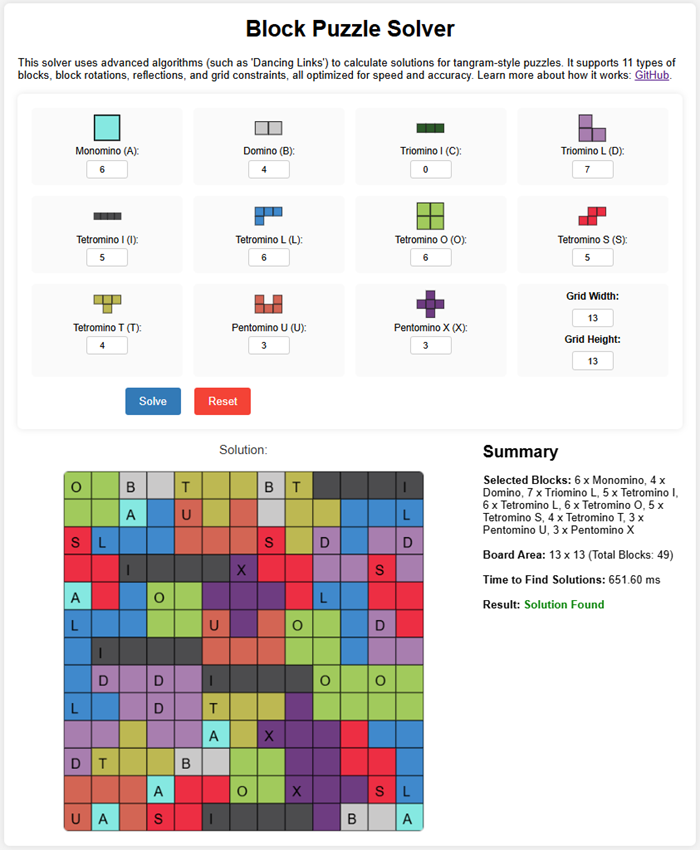
Update Nov 23, 2024:

I've created a new version of The Block Puzzle Solver that solves tangram and tetris-style puzzles using slightly more efficient algorithms (such as the Dancing Links method). This new solver supports 11 block types and considers rotations, reflections, and grid constraints to optimize the solution.

https://github.com/JozefJarosciak/TangramPuzzleSolver

Features

  • Dynamic Block Configuration: Select and configure different types of blocks (e.g., Monomino, Domino, Tetromino).

  • Grid Adaptability: Automatically computes the best-fit grid dimensions based on the selected blocks.

  • Visualization: Interactive visual display of the solution on an HTML5 canvas.

  • Timeout Handling: Ensures solutions are computed within a reasonable time frame.

Demo