Java offers eight primitive data types which are not always adequate to store data of all types. There are situations when the specific data type does not fit into any of the primitive data types offered by Java. Thus it is essential to understand the boundaries and restrictions of the primitive data types in Java. In this article, I demonstrate a couple of the scenarios in which the Java data types are not sufficient enough and require substitute approach.

Java Data Types

This article concerns primarily with Java’s primitive data types, that can be either numeric or non-numeric. Primitive numeric data types are split into ‘numeric integer’ or ‘numeric floating point.’ Numeric integer data types are following: byte (8 bit), short (16 bit), integer (32 bit) and long (64 bit), while numeric floating-point types are float (32 bit) and double (64 bit).

I have created a graphical representation (Figure 1) of Java’s primitive and non-primitive data types along with the bit representation of the size available to each one of them.

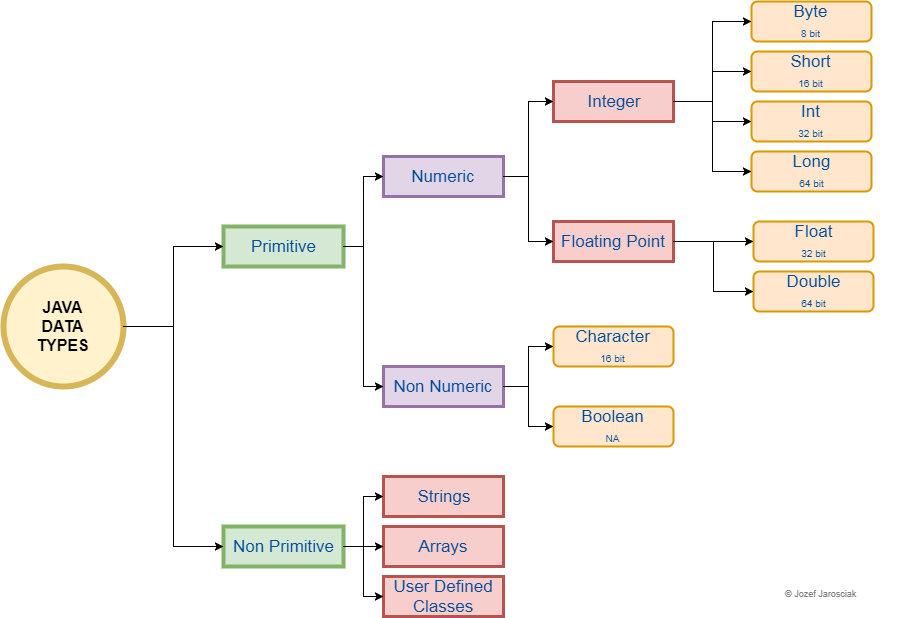
Figure 1 - (Jarosciak, 2018)

Lower and Upper Boundaries of Java Primitive Data Types

To explore the boundaries of numeric integer and numeric floating data types, and to prove that they are in fact imposed on Java developers, let's write a short Java program that prints the limits directly into the console (Figure 2).

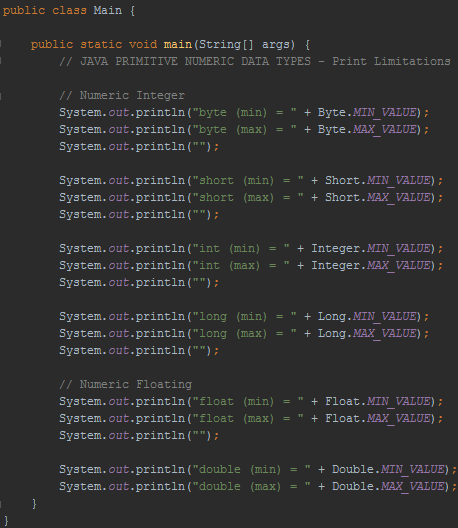
Figure 2 - (Jarosciak, 2018)

Figure 3 shows the output and illustrates the upper and lower confines of Java primitive data types. As we can see, all of the numeric primitive data types differ by their lower and upper boundaries. It is easy to realize that the margins imposed by Java data types may either positively or negatively impact all Java developers.

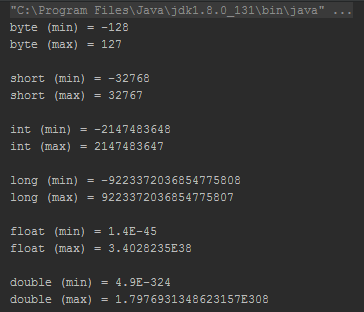
Figure 3 - (Jarosciak, 2018)

The Limitations of Primitive Data Types

In the following section, I go over some of the use cases to illustrate that we need to consider limitations of Java’s eight primitive data types in software development.

Case #1: 8-bit Signed Integer (byte)

As we could see shown in Figure 3, ‘byte’ data type takes values between -128 and 127. Assigning a numerical value smaller than -128 or larger than 127 to 8-bit signed integer data type would produce an error.

To test the theory, I assigned the number 128 to the variable ‘a’ with byte data type (Figure 4).

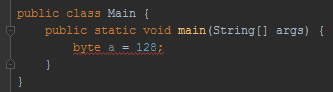
Figure 4 - (Jarosciak, 2018)

Figure 5 shows that code produces error reporting that number assigned to var ‘a’ is of an incompatible type.

Figure 5 - (Jarosciak, 2018)

Likely the finest way to fix the problem without occupying too many bites of storage is to change the variable ‘a’ from byte type to short signed integer data type. So instead of byte a = 128; we would write: short a = 128;

We could select integer (size: 32 bit) and write int a = 128; but the short type is more elegant, as it only takes 16 bits of storage.

Case #2: Character (char)

“A Java character is represented as two bytes” (Malek et al., 2006). Char is a non-numeric primitive data type we can explore. Let’s assign letter ‘a’ or Unicode representation of single char variable (such as ‘\u0055’ or number 85) all these will be accepted by char variable and print as expected (Figure 6). In fact, any special character (such as ‘Ď’), as long as it is a single character in Basic Multilingual Plane (BMP), it will be fully supported by char.

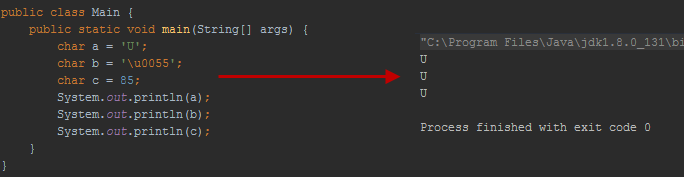
Figure 6 - (Jarosciak, 2018)

However, adding two letters to char would produce an error, because char is limited to 16 bits that are good enough only to fit a single character. The solution for 2 and more characters is to move from the single character limitation of char data type and use non-primitive ‘String’ data type.

The char data type can only hold 16-bit entities. So the number of characters it can take is limited. When it was invented originally as a data type, it was based on the Unicode specification (fixed-width 1).

Essentially said, CHAR only supports Basic Multilingual Plane (BMP), and those are the values from U+0000 to U+FFFF only and neither of the characters with codes that are larger than U+FFFF (btw. these are called supplementary characters).

However, as the time went, also the Unicode Standard has evolved and supports characters over 16 bits in the Unicode scalar value range of U+0000 to U+10FFFF.

Oracle documentation says: "A char value, therefore, represents Basic Multilingual Plane (BMP) code points, including the surrogate code points, or code units of the UTF-16 encoding. An int value represents all Unicode code points, including supplementary code points. The lower (least significant) 21 bits of int are used to represent Unicode code points and the upper (most significant) 11 bits must be zero. Unless otherwise specified, the behavior with respect to supplementary characters and surrogate char values is as follows:

- The methods that only accept a char value cannot support supplementary characters. They treat char values from the surrogate ranges as undefined characters. For example, Character.isLetter('\uD840') returns false, even though this specific value if followed by any low-surrogate value in a string would represent a letter.

- The methods that accept an int value support all Unicode characters, including supplementary characters. For example, Character.isLetter(0x2F81A) returns true because the code point value represents a letter (a CJK ideograph).

In the Java SE API documentation, Unicode code point is used for character values in the range between U+0000 and U+10FFFF, and Unicode code unit is used for 16-bit char values that are code units of the UTF-16 encoding. " (Docs.oracle.com, 2018)

You have asked: "I would like to hear from you when do you think we should use the char data types in Java code?".

"Primitive types in Java have advantages in term of speed and memory footprint." (Parodi, 2018). Other than the memory footprint benefits, in my view, char with its two-byte representation (16 bit) is still a valuable data type anywhere where developers expect to deal only with the single characters in the Basic Multilingual Plane (BMP) and don't want to use full-blown String object.  

Case #3: Real Number Double Precision (double)

“The loss of accuracy that results from approximating a real number by a floating point number is likely to be amplified.” (Clinger, 1990).

A floating-point number signifies a limited-precision rational number with the possible fractional part, and due to limited accuracy, only a subgroup of real and rational number is supported; other numbers can only be approximated. This is shown in Figure 7; we can see the inefficiency of using double for currency calculations. Solution is to

Figure 7 - (Jarosciak, 2018)

The accommodating solution would use the BigDecimal class that supports the exact depiction of decimal values.

Case #4: Signed Integer (int)

Integer in Java supports 32 bit long numbers (4 bytes), any number below -2,147,483,648 and above +2,147,483,647 will generate error. The solution is to move to a 64-bit space and use datatype Signed Long Integer (Long) with a maximum of over 10^18.

Case #5: Signed Long Integer (Long)

Long integer in Java supports 64-bit long numbers (8 bytes), but inserting any number below -9223372036854775807 or above +9223372036854775807 generates an error. The solution is to import java.math.BigInteger class that supports large integers, then the code works as illustrated in Figure 8.

Figure 8 - (Jarosciak, 2018)

TEST

I wrote the following (Figure 1) Java program to demonstrate the Overflow and Underflow in Java numerical data types:

package com.jarosciak.checkoverflow;

import static java.lang.System.out;

public class Main { public static void main(String[] args) { // BYTE Overflow & Undeflow byte byteTest = Byte.MAX_VALUE;byteTest++; out.println("Byte Overflow: " + Byte.MAX_VALUE + " + 1 = " + byteTest); byteTest = Byte.MIN_VALUE;byteTest--; out.println("Byte Undeflow: " + Byte.MIN_VALUE + " - 1 = " + byteTest); out.println("");

    // SHORT Overflow & Undeflow
    short shortTest = Short.MAX_VALUE;shortTest++; out.println("Short Overflow: " + Short.MAX_VALUE + " + 1 = " + shortTest);
    shortTest = Short.MIN_VALUE;shortTest--; out.println("Short Undeflow: " + Short.MIN_VALUE + " - 1 = " + shortTest); out.println("");

    // INTEGER Overflow & Undeflow
    int intTest = Integer.MAX_VALUE;intTest++; out.println("Integer Overflow: " + Integer.MAX_VALUE + " + 1 = " + intTest);
    intTest = Integer.MIN_VALUE;intTest--; out.println("Integer Undeflow: " + Integer.MIN_VALUE + " - 1 = " + intTest); out.println("");

    // LONG Overflow & Undeflow
    long longTest = Long.MAX_VALUE;longTest++; out.println("Long Overflow: " + Long.MAX_VALUE + " + 1 = " + longTest);
    longTest = Long.MIN_VALUE;longTest--; out.println("Long Undeflow: " + Long.MIN_VALUE + " - 1 = " + longTest); out.println("");

    // Float Overflow & Undeflow
    float floatTest = Float.MAX_VALUE;floatTest++; out.println("Float Overflow: " + Float.MAX_VALUE + " + 1 = " + floatTest);
    floatTest = Float.MIN_VALUE;floatTest--; out.println("Float Undeflow: " + Float.MIN_VALUE + " - 1 = " + floatTest); out.println("");

    // Double Overflow & Undeflow
    double doubleTest = Double.MAX_VALUE;doubleTest++; out.println("Double Overflow: " + Double.MAX_VALUE + " + 1 = " + doubleTest);
    doubleTest = Double.MIN_VALUE;doubleTest--; out.println("Double Undeflow: " + Double.MIN_VALUE + " - 1 = " + doubleTest); out.println("");
}

}

The output of the Java program (Figure 2) shows that for byte, short, integer and long, we are getting expected results for both underflow and overflow situation:

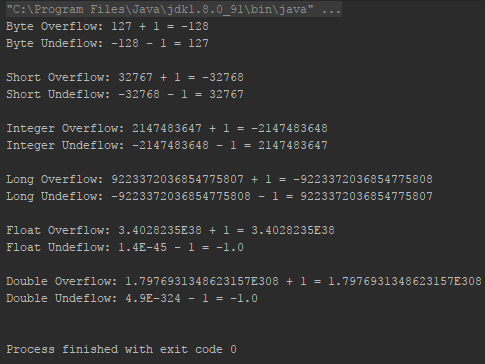
So, the following looks exactly how it should and indeed, the overflow and underflow definitely applies to other numerical data types

Byte Overflow: 127 + 1 = -128 and Byte Undeflow: -128 - 1 = 127

Short Overflow: 32767 + 1 = -32768 and Short Undeflow: -32768 - 1 = 32767

Integer Overflow: 2147483647 + 1 = -2147483648 and Integer Undeflow: -2147483648 - 1 = 2147483647

Long Overflow: 9223372036854775807 + 1 = -9223372036854775808 and Long Undeflow: -9223372036854775808 - 1 = 9223372036854775807

However, when it comes to Float and Double we see:

Float Overflow: 3.4028235E38 + 1 = 3.4028235E38

And it also gets an interesting result for underflow when subtracting 1 from the minimum value:

Float Underflow: 1.4E-45 - 1 = -1.0

The same thing with Double:

Double Overflow: 1.7976931348623157E308 + 1 = 1.7976931348623157E308

Double Undeflow: 4.9E-324 - 1 = -1.0

This is due to the floating-point data types and their different binary format: sign bit, exponent & mantissa.

These "weird" results are not really specific to Java. Floats are defined by the IEEE standard to which many other languages adhere.

In our specific results: Float.MIN_VALUE is the smallest positive float, so it's very close to 0. Hence Float.MIN_VALUE - 1 will be very close to -1. But since the float precision around -1 is greater than that difference, it comes out as -1. As to Float.MAX_VALUE, the float precision around this value is much greater than 1 and adding one doesn't change the result.

A case for primitive data types

The primitive data types are the controversial feature of Java and often considered a weakness ever since they were added to Java programming language in its initial release in 1996.

Sherman R. Alpert from IBM T.J. Watson Research Center in his paper that originally appeared in Java Report, November 1998 (Volume 3, Number 11), claimed that Java designers included primitive types only to be consistent with C++, because Bjarne Stroustrup, C++’s designer, wanted to be as consistent as possible with the base C language. He says: "For Java, this is a debatable issue. There is no base language with which Java ought to be consistent." (Research.ibm.com, 2018).

15 years later, in 2011; the issue of using primitive data types in Java grew to such proportions, that at JAX London, keynote speaker Simon Ritter (then Head of Java Technology at Oracle Corporation) mentioned that serious consideration was given to the removal of primitives in a future version of Java. As we can see, this has been a source of debate since 1996.

More recently, Dr. John Moore, Professor of Mathematics and Computer Science at The Citadel, says: "With primitive types, there is only one reason to use them — performance; and then only if the application is the kind that can benefit from their use. Primitives offer little value to most business-related and Internet applications that use a client-server programming model with a database on the backend. But the performance of applications that are dominated by numerical calculations can benefit greatly from the use of primitives." John I. Moore, J. (2018)

I must say I agree, the issue of performance in specific applications can be quite important. Recently, JavaWorld compared the runtime performances for primitives and objects using the algorithm for multiplying two matrices of type double. The conclusion is shown below, "The runtime performance of double is more than four times as fast as that of Double. That is simply too much of a difference to ignore." (Moore, 2018).

Conclusion

Sherman R. Alpert, a researcher from IBM T.J. Watson Research Center, states*” ‘100% Java’ is the Java developers’ slogan, meaning ‘Don’t taint your Java software by incorporating non-Java components’… At one particular juncture, I believe the language architects made the wrong choice, and that was the decision to incorporate non-object primitive types into the otherwise uniform object-oriented language model… Primitive types, as is, bear multiple disadvantages for object-oriented—and, specifically, Java—programmers.”* (Alpert, 2018).

The negative sentiment comes primarily due to limitations imposed by primitive numeric data types. For example, JavaScript is ‘loosely typed’ language, meaning it has no static types. This is in my view a weakness and languages such as TypeScript are a proof that strongly typed data types had to be invented to introduce type safety into JavaScript.

“Java is strongly typed language, which means that every variable and every expression has a type that is known at compile time.” (Hassanzadeh and Mosher, 1996).

Some researchers do not like non-object types in OOP language, but in my view, it is a benefit, because it provides developers with the assurance that once a variable is allocated to its data type and is within its imposed limitations, a variable will never behave in an unexpected way.

References

Alpert S.R. (2018). Primitive Types Considered Harmful. [online] Available at: https://www.research.ibm.com/people/a/alpert/ptch/ptch.html [Accessed 18 Jan. 2018].

Clinger, W. D. (1990). How to read floating point numbers accurately (Vol. 25, No. 6, pp. 92-101). ACM.

Malek, S., Seo, C., & Medvidovic, N. (2006, November). Tailoring an architectural middleware platform to a heterogeneous embedded environment. In Proceedings of the 6th international workshop on Software engineering and middleware (pp. 63-70). ACM.

Hassanzadeh, S., & Mosher, C. C. (1996). Java: Object-Oriented programming for the cyber age. The Leading Edge, 15(12), 1379-1381.

Docs.oracle.com. (2018). Character (Java Platform SE 8 ). [online] Available at: https://docs.oracle.com/javase/8/docs/api/java/lang/Character.html [Accessed 21 Jan. 2018].

Parodi, A. (2018). Difference between "char" and "String" in Java. [online] Stackoverflow.com. Available at: https://stackoverflow.com/questions/10430043/difference-between-char-and-string-in-java [Accessed 21 Jan. 2018].

John I. Moore, J. (2018). A case for keeping primitives in Java. [online] JavaWorld. Available at: https://www.javaworld.com/article/2150208/java-language/a-case-for-keeping-primitives-in-java.html [Accessed 23 Jan. 2018].

Research.ibm.com. (2018). Primitive Types Considered Harmful. [online] Available at: https://www.research.ibm.com/people/a/alpert/ptch/ptch.html [Accessed 23 Jan. 2018].